Overview of Sampling Design

What is Sampling Design?

Sampling design refers to the structured approach used to select a subset of data points or observations from a larger population or dataset. A well-thought-out sampling design ensures that the selected sample is representative of the broader population, reducing bias and improving the reliability of results.

The design includes several key dedision points such as the:

  • total sample size (number of samples)
  • sampling unit (size and shape of each sample)
  • sampling technique (e.g. random, gridded, proportional allocation across strata)
  • method of sample distribution (tool used to assign sample locations)

How is sampling used?

Sampling design has uses in many fields, but we will be focusing on three main use cases:

  • Gathering samples for training machine learning algorithms
  • A statistical approach used to infer the characteristics of a larger area or population by analyzing data from a representative subset (sample) of that area
    • Namely, sample-based area estimation, for estimating areas of a feature and quantifying uncertainties, avoiding the bias inherent in using maps for area estimation
  • Extracting samples for accuracy assessment of a map

What are the goals of a good sampling design?

  1. Representativeness
    • Ensure the sample accurately reflects the population or area of interest.
    • Include all key subgroups or characteristics to avoid bias.
    • Achieve proportional representation where needed, such as in stratified sampling.
    • Avoid over-representing specific regions or under-sampling others.
    • Ensure variability within each class is captured in the sample.
  2. Efficiency and Practicality
    • Maximize the accuracy and reliability of the estimates while minimizing resource use, such as time, cost, and effort.
    • Estimate the available resources and the number of samples needed to achieve goals early on in your design.
    • Some methods for improving efficiency include stratified sampling and systematic sampling.
  3. Unbiased Estimation
    • Avoid systematic errors in selecting or measuring samples.
    • Use probability-based methods to ensure each unit has a known and non-zero chance of selection, which should be recorded for later analyses.
  4. Flexibility
    • Allow for adaptability to unforeseen challenges during sampling, such as planning for iterative additional sampling.
    • Plan for potential integration of additional samples or modifications without compromising the design’s integrity.
  5. Validity for Analysis (Statistical and/or ML Model)
    • Allow for robust statistical analysis and meaningful inference about the population.
    • Ensure the sample size is adequate for achieving reliable estimates and uncertainties (when applicable).
    • For most statistical analyses important to our use case, at least 30 samples from the class of interest are necessary for reliable results. - Avoid over-fitting or under-fitting a machine learning model due to the number of training samples.
    • Overfitting occurs when a model learns patterns, noise, or anomalies specific to the training data, rather than generalizable patterns relevant to the entire population.
    • Underfitting occurs when a model fails to learn sufficient patterns from the data, resulting in poor model performance.
  6. Reproducibility
    • Design a sampling process that can be repeated by others for consistency and verification.
    • Use clear, documented procedures for sample selection and measurement.

Some Well Known Sampling Techniques

There are several different ways to sample an area in order to achieve a representative sample or the landscape and the variations within it. Here are a few ways to distribute samples.

Systematic Sampling: observations are placed at equal intervals according to a strategy

Simple Random Sampling: observations randomly placed

Stratified Random Sampling: Using a map to inform the design, a minimum number of observations randomly placed in each category

Stratified random sampling has two key benefits

  • Updates map-based areas to increase precision (reduces uncertainty)
  • Helps increase chance of having plots in rare classes

Use cases for sampling

Use 1: How samples are used as training data for a machine learning algorithm

In simple terms, training data is the information a machine learning algorithm uses to “learn” how to make predictions or decisions.

  • The training samples are like the examples to a teacher provides to a student. The sample data includes:
    • the inputs, which are the features and/or associated variables for the sample,
    • and the “outputs”, which are the correct labels for the samples.

  • The algorithm looks at the training data and tries to figure out the rules or patterns that connect the inputs to the outputs

  • Using the patterns it finds, the algorithm builds a model. A model is like a set of rules or a formula that can predict the output for new, unseen inputs.

  • Once the model is sufficiently trained, it can be used to make predictions on new data that does not have provided labels.

In summary, a machine learning algorithm uses training data to learn patterns and create a model that can predict/classify new information.

Simple Example

Imagine teaching a child to identify apples:

  • Training Data: You show the child pictures of apples and oranges and tell them which is which.
  • Learning: The kid notices patterns (apples are round, red or green, and have a stem).
  • Model: The kid forms a mental “rule” to identify apples.
  • Prediction: When shown a new fruit, the kid uses their rule to decide if it’s an apple.

Sampling design considerations for ML algorithm training

For training machine learning algorithms, sampling design is critical to ensure that the data used to train the model covers the variability in the dataset, preventing overfitting or underfitting. Sometimes the full data set of samples is split into training and testing subsets to evaluate model performance, but separate sampling design for the validation data can also be done. Anything you want the ML algorithm to learn, should be provided as an example in the training samples.

General rules of thumb to use for sampling design to gather training data for Random Forest:

  • A commonly cited rule is to have at least 10 times as many samples as there are features (variables) in the dataset to provide enough data for the model to learn meaningful patterns.
    • Example: For 20 features, aim for at least 200 samples per class
  • Decide on a minimum number of samples per class:
    • For simple problems, aim for 50–100 samples per class.
    • For complex problems or high-dimensional datasets, aim for 500–1,000 samples per class or more.
  • Classes with fewer samples (minority classes) should have a minimum of 30–50 samples to ensure meaningful learning.
  • Highly variabile classs requires larger sample sizes to capture the diversity.

Use 2: Inferring characteristics of a population based on a sample (e.g. sample-based area estimation)

Historically, maps have been used to quantify the area of each class by pixel counting. Pixel counting approaches simply sum up the area belonging to each class.

  • However, this method is prone to bias due to classification errors (e.g., data noise, pixel mixing, or poor class separation).
  • Pixel counting can result in over- or underestimates, and you cannot quantify this uncertainty.

Sample-based approaches use manually collected samples and statistical formulas based on the sampling design to estimate class areas.

  • Uses manually collected reference samples (typically collected in a program like CEO) and statistical methods to estimate class areas.
  • The sample data is used to make estimates for for the whole area of interest.
  • Provides unbiased estimates and quantifies errors, making results more reliable and robust.

Sampling design considerations for quantifying the characteristics of a popultation

Probability-based methods of sampling are used to ensure each unit has a known and non-zero chance of selection, which is required for statistical analysis and uncertainty estimations. The major objective of the sample is to provide information that is representative of the full population.

In sample-based area estimation, such as estimating forest cover, a representative sampling design ensures accurate population metrics while minimizing variance and resource use. The selected type of sampling design is tailored to the study’s objectives and constraints.

A map is not necessary for selecting sample locations but it makes the representative sampling process far more efficient when you are looking at a characteristic of interest with a geographically small area within the population, reducing the total number of points you need to collect to meet your desired level of uncertainty in your estimates.

Use 3: Map validation (accuracy assessment)

  • Map validation compares map class labels at sample points to reference data labels, considered the reference data to be “correct” values.
  • The reference labels are typically based on human interpretations of imagery.
  • High agreement between map labels and reference labels indicates the map accurately represents the mapped characteristics.
  • Accuracy is often assessed using a confusion matrix (error matrix). This will be explained further later in the workshop.

Sampling design considerations for map accuracy assessments

Random Sampling option:

  • Goal: A random sample allows for simple analysis using a confusion matrix.
  • Impact: Rare classes in the map may have too few points for meaningful accuracy analysis.
  • Consideration: You should have at least 30 samples per class for robust and statistically valid results, so you may need to distrinute a lot of random samples to achieve this if you have rare classes.

Stratified Sampling option:

  • Goal: Ensures sufficient points (e.g., >30) for rare classes by sampling disproportionately across strata.
  • Impact: Stratified sampling introduces unequal sample sizes, so although helpful for class-specific accuracy (allows >30 points per strata), it can skew overall accuracy assessments if not correctly weighted
  • Consideration: In order to adjust for this unequal distribution you must use a slightly more complicated analysis for your overall accuracy, by weighting class-specific accuracy based on the area proportions.

Note… The samples you are using for training the machine learning algorithm CANNOT also be used or for map validation. This must be a completely separate set of points. When you validate with training data, the accuracy is typically much higher than it would be for new, unseen data because the model is evaluated on the same information it was trained to replicate.



Futher explanation of statistical details

The >30 samples rule

The Central Limit Theorem states that, for a sufficiently large sample size (commonly 30 or more), the sampling distribution of the sample mean approaches a normal distribution, regardless of the population’s actual distribution. This normality assumption is crucial for many statistical tests and confidence interval calculations used in accuracy assessments. With smaller sample sizes, the estimates of accuracy (e.g., overall accuracy, producer’s accuracy, user’s accuracy) can vary widely, leading to unreliable or unstable results.

Using a Confusion Matrix (simple unweighted example)

We can quantify the accuracy of the map using a confusion matrix (error matrix). The reference data dictates the actual value (the truth) while the left shows the prediction (or map classification). - True positive and true negative mean that the classification correctly classified the labels (e.g., a flood pixel was correctly classified as flood). - False positive and false negative mean that the classification does not match the truth (e.g., a flood pixel was classified as no-flood)

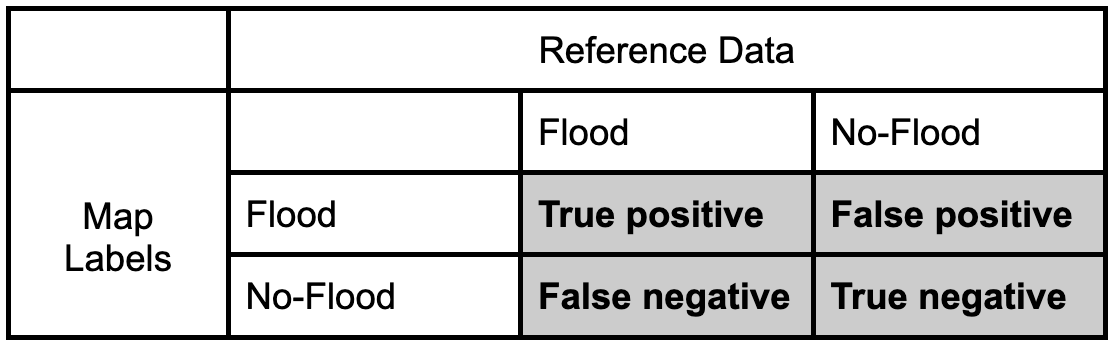
Let’s fill in this confusion matrix with example values if 100 points were collected.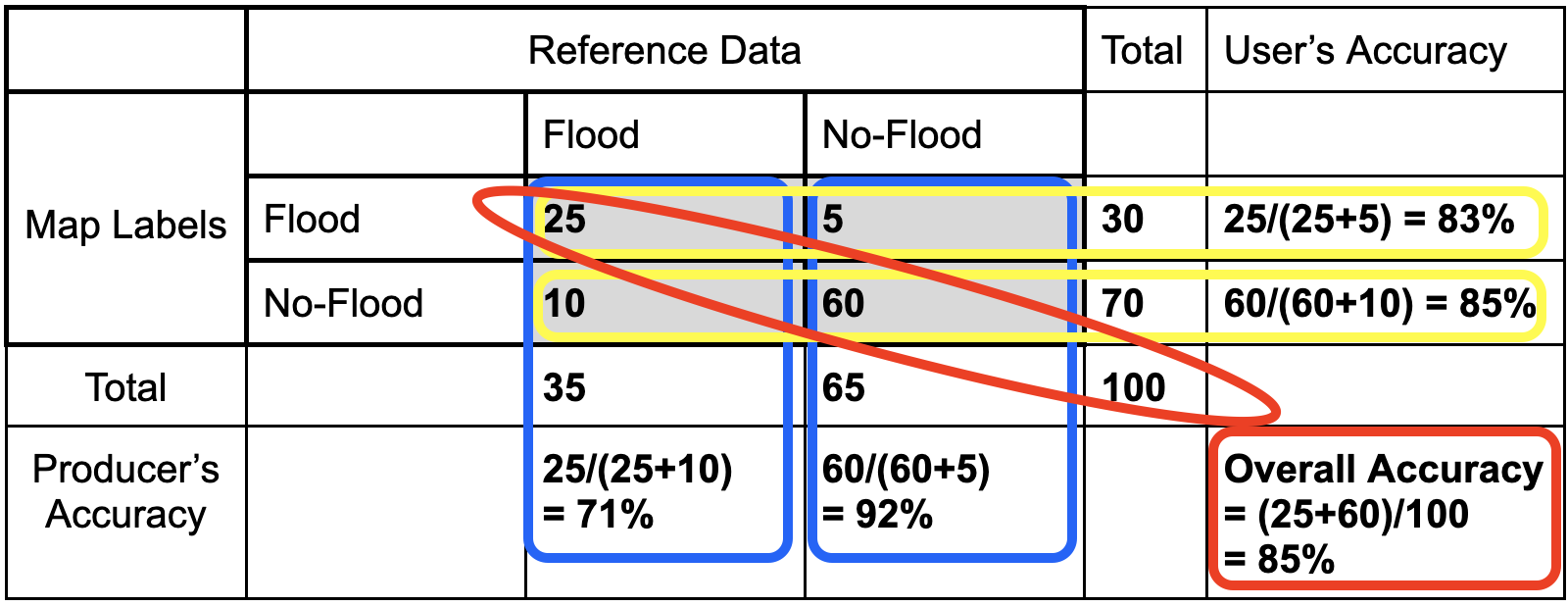

Producer’s Accuracy

  • The percentage of time a class identified on the ground is classified into the same category on the map. The producer’s accuracy is the map accuracy from the point of view of the map maker (producer) and is calculated as the number of correctly identified pixels of a given class divided by the total number of pixels in that reference class. The producer’s accuracy tells us that for a given class in the reference pixels, how many pixels on the map were classified correctly. The percentage of time a class identified on the ground is classified into the same category on the map.
  • Producer’s Accuracy (for flood) = True Positive / (True Positive +False Positive)
  • Producer’s Accuracy (for no-flood) = True Negative / (True Negative +False Negative)
  • On a confusion matrix, for each class it is the… on-the-diagonal value / column’s sum.

Omission Error

  • Omission errors refer to the reference pixels that were left out (or omitted) from the correct class in the classified map. An error of omission will be counted as an error of commission in another class. (complementary to the producer’s accuracy)
  • Omission error = 100% - Producer’s Accuracy
  • (Flood) Omission Error is when ‘flood’ is classified as some ‘other’ category.

User’s Accuracy

  • The percentage of time a class identified on the map is classified into the same category on the ground. The user’s accuracy is the accuracy from the point of view of a map user, not the map maker, and is calculated as the number correctly identified in a given map class divided by the number claimed to be in that map class. The user’s accuracy essentially tells us how often the class on the map is actually that class on the ground. The percentage of time a class identified on the map is classified into the same category on the ground.
  • User’s Accuracy (for flood) = True Positive / (True Positive +False Negative)
  • User’s Accuracy (for no-flood) = True Negative / (True Negative +False Positive)
  • On a confusion matrix, for each class it is the… on-the-diagonal value / row’s sum.

Commission Error

  • Commission errors refer to the class pixels that were erroneously classified in the map. (complementary to the user’s accuracy)
  • Commission error = 100% - user’s accuracy.
  • (Flood) Commission Error is when ‘other’ is classified as ‘flood’.

Overall Accuracy

  • Overall accuracy = (True Positive + True Negative) / Sample size
  • The overall accuracy essentially tells us what proportion of the reference data was classified correctly
  • On a confusion matrix, it is the… sum of all on-the-diagonal values.



Sources

Table of contents

2025 --- Spatial Informatics Group / NovaSphere --- Financial support from Environment and Climate Change Canada